姫慄偲丄媩偺廳怱偺娭學丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
僪僀僣丒償傽僀僆儕儞惢嶌儅僀僗僞乕丂嵅乆栘楴丂
媩偺廳怱堏摦偺寁嶼曽朄
丂廳怱偼偦傟偧傟偺幙揰宯偵偮偄偰丄偦偺乽幙検亊嫍棧乿傪媮傔丄偦傟傪懌偟崌傢偣丄偦偟偰慡懱偺幙検偱妱偭偨傕偺偲偟偰媮傔傞偙偲偑偱偒傞丅偙傟傪暔棟妛揑偵彂偔偲丄師偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂丂丂丂儼r倝m倝
丂丂廳怱偺嵗昗丂俧亖劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂儼m倝
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂m倝丗幙揰倝偺幙検
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂r倝丗婎弨嵗昗偐傜幙揰m倝傑偱偺嫍棧
丂偙偺幃傪墳梡偡傞偲丄嬧慄傪姫偔慜偵偍偄偰丄媩偺廳怱傪寁嶼偱惓妋偵梊應偡傞偙偲偑偱偒傞偺偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂儼r倝m倝亄rm
丂丂丂丂丂堏摦偟偨廳怱偺嫍棧俧亖劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂M亄m
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂M丗姫慄側偟偺媩偺廳偝
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂m丗姫慄偺廳偝
偙偙偱姫慄偺廳偝傪愊暘偵傛偭偰摫偔偲丄忋偺幃偼師偺傛偆偵曄宍偝傟傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂儼r倝m倝亄佺r冃dr
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖劅劅劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂M亄m丂丂丂丂丂丂丂丂丂冃丗扨埵挿偝偁偨傝偺姫慄偺廳偝
丂姫慄傪姫偄偰偄側偄忬懺偱丄廳怱偺偲傟偨埵抲傪婎弨揰乮俧侽乯偲偡傞偲丄儼r倝m倝亖侽偲偄偆偙偲偑傢偐傞偺偱丄忋偺幃偼丄嵟廔揑偵師偺傛偆偵姫慄偺愊暘偩偗偺娙扨側幃偵曄宍偝傟傞丅廬偭偰丄廳梫側抣偲偟偰冃乮侾mm暆姫偄偨帪偺姫慄偺幙検乯傪媮傔傞偙偲偑昁梫偵側偭偰偔傞偺偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂佺r冃dr
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖劅劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂M亄m
侾mm暆姫偄偨帪偺姫慄偺幙検冃偺媮傔曽
冃傪媮傔傞偨傔偵偼丄師偺偙偲偑傢偐傜側偗傟偽側傜側偄丅
丂丒姫慄偺捈宎丂
丂丒姫慄偺慄枾搙乮姫慄侾倣偁偨傝偺幙検乯
師偼偙傟傜偺媮傔曽偵偮偄偰丄弴偵愢柧偟偰偄偔丅
侾丒姫慄偺捈宎偲丄慄枾搙
| 姫慄偺庬椶 | 枾搙 | 慄枾搙 |
| 梞嬧慄 | 冇 0.250mm | 0.427g/m |
| 嬧慄乮懢乯 | 冇 0.300mm | 0.741g/m |
| 丂乂乮嵶乯 | 冇 0.250mm | 0.441g/m |
| 嬧巺慄 | 冇 0.500mm | 0.389g/m |
| 丂乂丂 | 冇 0.375mm | 0.236g/m |
| 嬥慄18K乮懢 | 冇 0.300mm | 1.014g/m (Au75% Ag15% Cu10%) |
| 丂乂 乮嵶 | 冇 0.250mm | 0.604g/m |
| 嬥慄14K乮懢 | 冇 0.300mm | 0.853g/m (Au59% Ag12% Cu25%) |
| 乂 乮嵶 | 冇 0.250mm | 0.508g/m |
| 寏偺傂偘丂丂 | - | 1.053g/m (暆1.6mm 岤傒0.6mm) |
丂偙傟傜偺抣偼幚應偱媮傔偨乮嬥慄偼寁嶼偵傛偭偰乯丅偙偺昞傪傒傞偲丄嬥慄偲嬧慄偺懢偄曽偑旘傃敳偗偰廳偄偲偄偆偙偲偑傢偐傞丅傑偨丄嬧巺慄偼懢偄偵傕娭傢傜偢丄廳偝偼寉偄偲偄偆偙偲傕傢偐傞丅捈宎侽.俀俆mm偺嬧慄偲梞嬧慄偼丄廳偝偺柺偐傜偩偗尒傟偽摨幙偺傕偺偱偁傞偲峫偊偰傛偄丅丂拲堄偡傞揰偲偟偰丄忋婰偺慄枾搙偺妱崌偼丄捈愙丄廳怱堏摦偺妱崌偵寢傃偮偔傕偺偱偼側偄丅側偤側傜懢偄姫慄偼廳偄偑丄懢偄傇傫偩偗姫偒晅偗傞挿偝偑抁偔偰傕偡傓偐傜偱偁傞乮寏偺傂偘偼傛傝堦憌偦偆偱偁傞乯丅偙偺俀偮偺娭學偑偙傟偐傜峴側偆寁嶼偵傛偭偰惓妋偵媮傔傜傟傞偺偩丅
俀丒姫慄偺挿偝偺寁嶼曽朄乮嶲峫乯
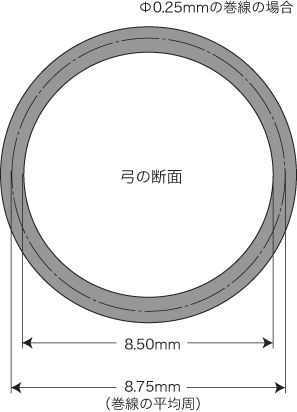
丂姫慄偺挿偝偼丄幚嵺偵姫偄偨傕偺傪夝偄偰應傞偺偑傛偄偑丄偦傟偼幚梡揑偱側偄偺偱丄寁嶼偵傛偭偰嬤帡揑偵媮傔傞曽朄傪偲傞丅偦偙偱傑偢偼丄姫慄傪堦廃姫偔偲偳傟傎偳偺挿偝偵側傞偐傪峫偊傞丅墌偺堦廃偺挿偝偼丄乽捈宎亊俁.侾係乿偱媮傔傞偙偲偑偱偒傞偑丄幚嵺偼恾偺傛偆偵丄嬧慄偺拞怱偼捈宎傛傝傕奜懁偵偁傞偺偱丄揰慄偺挿偝偼師偺幃偱媮傔傜傟傞丅
丂姫慄偺堦廃偺挿偝亖乮媩偺捈宎亄姫慄偺捈宎乯亊俁.侾係

丂偙傟偱堦廃偺挿偝偑媮傑偭偨偺偱丄師偼偦傟偑壗廃姫偐傟偰偄傞偐偱偁傞丅侾mm暆偵擖傞姫慄偺悢偼丄乽侾mm乛姫慄偺捈宎乿偱偁傝丄偙傟偵姫偄偨嬫娫偺挿偝傪偐偗傞偲姫慄偺姫偄偨挿偝偑偱偰偔傞丅傛偭偰傑偲傔傞偲丄
姫慄偺挿偝 亖乮堦廃偺挿偝乯亊乮侾mm乛姫慄偺捈宎乯亊乮姫偄偨嬫娫偺挿偝乯
丂丂丂丂丂丂丂亖乮媩偺捈宎亄姫慄偺捈宎乯亊俁.侾係亊乮侾mm乛姫慄偺捈宎乯亊乮姫偄偨嬫娫偺挿偝乯
丂丂丂丂丂丂丂丂丂丂丂丂 乮媩偺捈宎亄姫慄偺捈宎乯亊乮姫偄偨嬫娫偺挿偝乯亊俁.侾係
丂丂丂 丂丂丂丂亖 劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 姫慄偺捈宎 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂拲堄丒丒丒扨埵偼mm偱偱偰偔傞丅
俁丒冃乮侾mm暆姫偄偨帪偺姫慄偺幙検乯偺媮傔曽
忋偺俀丒偱乽侾mm暆偵擖傞姫慄偺姫偔悢偼丄乮侾mm乛姫慄偺捈宎乯偱媮傔偨丅廬偭偰偦偺暆偺姫慄偺挿偝偼丄
侾mm暆偺姫慄偺挿偝亖乮堦廃偺挿偝乯亊乮侾mm乛姫慄偺捈宎乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙傟偵慄枾搙傪偐偗傞偲冃偑偱傞偺偱偁傞丅
冃亖乮堦廃偺挿偝乯亊乮侾mm乛姫慄偺捈宎乯亊乮慄枾搙乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺冃偑媮傔傜傟傟偽丄屻偼偄偪偽傫嵟弶偵弎傋偨愊暘偺幃傪幚峴偡傟偽傛偄偺偱偁傞丅
係丒廳怱偺堏摦嫍棧俧偺媮傔曽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂佺r冃dr
丂丂丂丂堏摦偟偨廳怱偺嫍棧俧亖劅劅劅劅劅劅 丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 M亄m
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 乵丂r俀冃乶倐 丂倎
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖劅劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂M亄m 丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂1/2冃乮b俀 -a俀乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖劅劅劅劅劅劅劅劅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 M亄m
丂堦曽姫慄慡懱偺廳偝偼丄乮慡挿亊慄枾搙乯側偺偱乽俀丒乿偱媮傔偨姫慄偺挿偝偺寁嶼傪棙梡偡傞丅偡傞偲乽倣乿偑媮傑傞丅
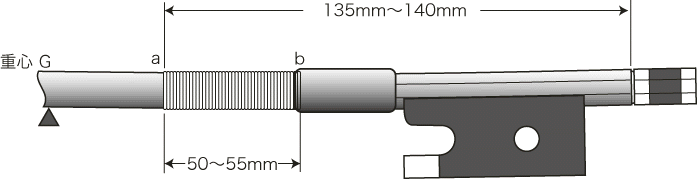
丂丂丂丂丂丂丂丂a丗嵟弶偺廳怱偐傜姫偒偼偠傔偺揰傑偱偺嫍棧
丂丂丂丂丂丂丂丂b丗嵟弶偺廳怱偐傜姫偒廔傢傝偺揰傑偱偺嫍棧
丂丂丂丂丂丂丂 丂M丗姫慄柍偟偺媩偺幙検
丂丂丂丂丂丂丂丂m丗姫慄偺廳偝丂
偙傟偐傜弎傋傞廳怱偺堏摦嫍棧偼丄偡傋偰偙偺幃偵傛偭偰摫偄偨傕偺偱偁傞丅
丂姫慄偺姫偔挿偝偺婎杮偼丄媩偺娖偺廔抂偐傜侾俁.俆噋乣侾係.侽噋傑偱偺栺俆侽mm乣俆俆mm娫偱偁傞丅乮搶嫗償傽僀僆儕儞惢嶌妛峑婎弨乯偙偺俆mm偺嵎偼屄恖偺岲傒偵傛傞丅廬偭偰偙偺嵎偑丄偳傟偩偗廳怱偺堏摦偵娭學偟偰偔傞偐偑嫽枴怺偄偲偙傠偱偁傞偑丄師偺昞偑偦偺寁嶼寢壥偱偁傞丅
| 姫慄偺庬椶 | 捈宎 | 廳怱堏摦嫍棧 乮俆侽mm乯 | 廳怱堏摦嫍棧 乮俆俆mm乯 |
| 嬧慄乮懢乯 | 0.300mm | -7.1mm | -7.6mm |
| 丂乂乮嵶乯 | 0.250mm | -5.1mm | -5.5mm |
| 嬧巺慄丂丂乂 | 0.375mm | -1.9mm | -2.0mm |
| 嬥慄14K乮懢) | 0.300mm | -8.1mm | -8.7mm |
| 乂 乮嵶) | 0.250mm | -5.9mm | -6.3mm |
| 寏偺傂偘 | 丂亅丂 | -2.0mm | -2.2mm |
丂偙傟傪尒傞偲丄俆mm懡偔姫慄傪姫偄偨妱偵偼丄廳怱偺堏摦偑彮側偄偲偄偊傞丅側偤側傜偽丄姫慄傪姫偒懌偟偨曽岦偑丄廳怱偵岦偐偭偰偩偐傜偱偁傞丅廳怱偺曄壔検偼丄摨偠廳偝偺傕偺傪壛偊偰傕丄廳怱偐傜墦偄暔傎偳戝偒偔側傞丅偙傟偱屄恖偺岲傒偵傛傞姫慄偺検偼丄偙偺埵偺堘偄偱偼梋傝偱側偄偙偲偑傢偐偭偨丅
姫慄傪廳偔偟夁偓傞晽挭偵偮偄偰
丂尰嵼偺棳峴偲偟偰丄媩偺廳偝傪姫慄傗僠僢僾偵傛偭偰憹偡偲偄偆曽朄偑偁偘傜傟傞丅柫媩偵摉傝慜偺傛偆偵侽.俁mm偺姫慄傪姫偄偨傝丄僠僢僾傪嬧偵庢傝懼偊偨傝偟偰偄傞丅偙偺傛偆側偙偲偵懳偟偰丄廳怱偑偳偆曄壔偟偰偄傞偐傪峫嶡偟偰傒傞丅
丂傑偢愭偺昞傪尒傞偲丄嬥慄偺廳怱堏摦検偑戝偒偄偙偲偑偡偖偵傢偐傞丅偟偐偟丄嬥慄偺応崌丄偦偺幙検偺戝偒偝偼扤偱傕抦偭偰偄傞偺偱丄拲堄怺偔庢傝埖傢傟傞丅偙傟偵懳偟偰婋尟側偺偼嬧慄偱偁傞丅嬧慄偺侽.俀俆mm偲侽.俁侽mm偼丄側傟偨恖偱側偄偲偡偖偵尒暘偗偑偮偐側偄偺偱丄彮乆廳偔偟偨偄応崌偵丄柍恄宱偵侽.俁mm偺嬧慄傪姫偄偰偟傑偆傛偆偩丅偟偐偟丄偦傟傜偺廳怱堏摦検偼栺係侽亾傕堘偭偰偄傞丅傕偲傕偲屆偄柫媩偼嬧巺慄傗丄寏偺傂偘偵傛偭偰僶儔儞僗傪偲傜傟偨傕偺側偺偱丄偙偺條偵姫慄偺廳偝偺憹壛偼丄傕偼傗尷奅偵偒偰偄傞丅偪側傒偵丄嬧巺慄偲寏偺傂偘偼廳怱偺柺偐傜偼摨幙偺暔偲傒偰傕傛偄丅
丂師偺恾偼姫偒旂偺壓傑偱嬧慄傪姫偄偨暔偱偁傞偑丄偙偆側傞偲榖偼傛傝怺崗偵側偭偰偔傞丅
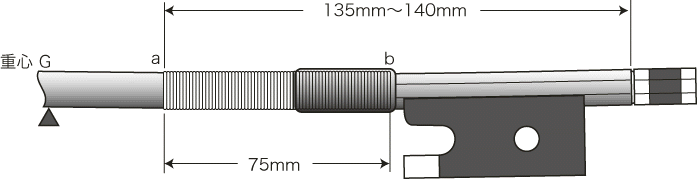
| 捈宎 | 俆侽mm | 姫旂壓傕 | |
| 嬧慄乮懢乯 | 冇 0.300mm | -5.1mm | -11.4mm |
| 乂乮嵶乯 | 冇 0.250mm | -5.1mm | -8.3mm |
廳怱偑侾們倣埲忋傕曄壔偡傞偲偄偆偙偲偼丄傕偼傗慡偔暿偺媩偵側偭偰偟傑偭偨偲峫偊偰傕丄戝偘偝偱偼側偄偺偱偼側偄偩傠偆偐乮偨偲偊墘憈朄偑曄傢偭偰偄傞偲偼偄偊乯丅
嬧僠僢僾偵傛傞廳怱偺曄壔
僠僢僾傪徾夊偐傜嬧偵姺偊偨応崌
丂丂丂丂徾夊僠僢僾丂0.25g丂
丂丂丂丂嬧僠僢僾 0.65g 乮岤傒0.5mm 乯
丂
丂愭傎偳偲摨偠寁嶼朄偵傛傝廳怱堏摦偺嵎傪媮傔傞偲丄嬧僠僢僾偵姺偊傞偙偲偵傛偭偰俧亖+3.7mm偲偄偆寢壥偑偱偨丅
丂僠僢僾偺埵抲偼廳怱揰傛傝棧傟偰偄傞偨傔偵丄傎傫偺侽.係倗偺嵎偱傕尠挊側嵎偲偟偰尰傢傟傞丅偙偺條偵僠僢僾偺廳偝偼丄侽.侾倗扨埵偱恄宱幙偵寛掕偟側偗傟偽側傜側偄丅傑偟偰丄僠僢僾偺拞偵墧傪媗傔傞偲偄偆偙偲偼丄師尦偺堘偆榖偲側傞丅
傑偲傔
丂偙傟傑偱廳怱偺堏摦検傪悢妛揑偵摫偄偰偒偨偑丄偙傟傪偄偪偄偪寁嶼偡傞偙偲偼尰幚揑偱側偄偺偱丄偍偍傛偦偺孹岦傪栚埨偵偡傟偽幚嵺偵偼廫暘偱偁傞丅
丂嬧慄偺侽.俀俆mm傪婎弨偲偟丄偦傟偵懳偟偰壗亾曄壔偡傞偐傪昞傢偟偨暔偱偁傞丅扐偟拲堄偡傞偙偲偲偟偰丄偙傟偼偦傟偧傟偺媩偺忦審偵傛偭偰旝柇偵堘偭偰偔傞丅
| 姫慄偺庬椶 | 丂捈宎丂 | 俆侽mm姫偄偨応崌 |
| 嬧慄乮懢乯 | 冇 0.300mm | 丂+2.0mm +39% |
| 丂乂乮婎弨乯 | 冇 0.250mm | 丂丂丂亅 |
| 嬧巺慄丂乂 | 冇 0.375mm | 丂-3.2mm -62% |
| 嬥慄14K乮懢) | 冇 0.300mm | 丂+3.0mm +59% |
| 乂 乮嵶) | 冇 0.250mm | 丂+0.8mm +16% |
| 寏偺傂偘丂 | 丂丂亅丂 | 丂-3.1mm -61% |
丂偙傟偵傛偭偰丄僶儔儞僗揑偵婎弨嬧慄偲摨偠偲峫偊傜傟傞偺偼丄侽.俀俆mm偺梞嬧慄偐侽.俀俆mm偺俉俲乣侾侽俲嬥慄偲偄偆偙偲偑傢偐傞丅偙傟埲奜偺姫慄傪巊梡偡傞応崌偵偼丄偦偺岠椡傪棟夝偟偨忋偱巊梡偟側偗傟偽媩偺廳怱埵抲偑曄傢偭偰偟傑偆偺偱丄拲堄偑昁梫偱偁傞丅